10/06/17 : Début de l'étude.

I) Étude théorique :

A) Rappel des données du cahier des charges

Si l'on reprends le cahier des charges on peut rassembler les données suivantes :

• Longueur total : 180cm
• Largeur utile : 35 cm 
• Largeur total : A déterminer
• Hauteur utile : 30cm
• Hauteur total : A déterminer
• Charge utile : 23 Kg

Donc, avec ces données, on peut commencer à travailler.

B) Un Dry Dock ou forme de radoub, qu'est-ce que c'est ?

Les navires et à fortiori les sous-marins ont besoin de pouvoir être entretenu hors de l'eau afin d'effectuer certains travaux sur la carène ou sur d'autre partie du bâtiment.

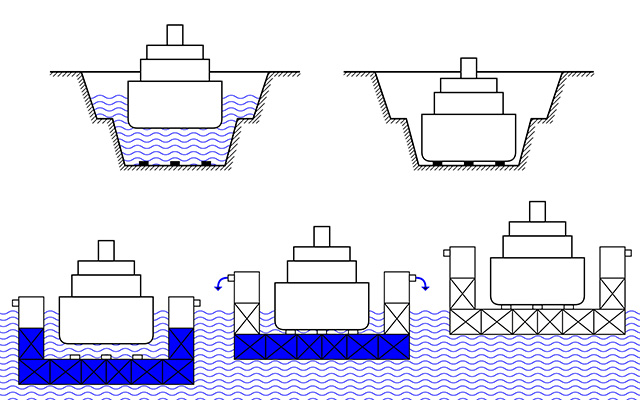
Sans refaire l'historique depuis les phéniciens, vous trouverez ça sur Wikipédia on va principalement s'intéresser à la version flottante, les formes fixes sont architecturalement très belle, mais dans notre cas pas très utile (à moins de l'inclure dans une piscine perso.... mais là... c'est le grand luxe ! :D ).

Donc, en gros un dock flottant, c'est un bateau dont la charge utile est égale au poids max des bâtiments que l'on veut entretenir et qu'on peu couler de façon contrôlé pour faire rentrer la charge utile. Naturellement, il existe deux versions, celle ou effectivement, c'est un bateau :

Très pratique pour transporter des bâtiments qui ont perdu leur capacités de propulsions. Ou alors les formes qui dépendent des tug boat (remorqueurs) pour être déplacé : 

C'est à cette deuxième catégories que je choisie de réaliser.

C) Un peu de théorie...

"Tout corps plongé dans la vodka en ressort bourré à hauteur du taux d'alcoolémie suite à l'ingestion de son volume de vodka déplacé !" Vladimir Archimèdeovitch

Je fait un raccourci dans la démonstrations en donnant l'une des valeurs qui à ce stade n'est pas encore déterminé à savoir la largeur total du dock.

Prenons un  volume parallélépipédique de dimensions : 180cmx47cmx1cm

Le volume est égal à 8460 cm3 soit 8,460 Litres.

Si on part du principe que ce parallélépipède est parfait et que sa masse est nul et qu'on le pose sur l'eau, il flotte et sa surface total est hors de l'eau [Fig. A].

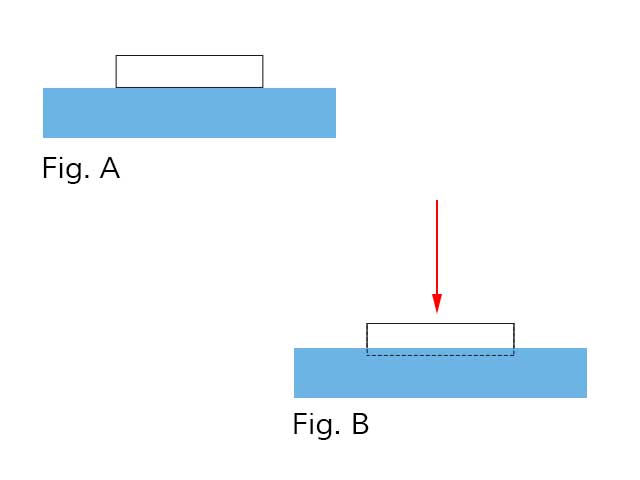
Maintenant, si à ce volume, on applique, disons une masse de 1Kg, le volume va s'enfoncer légèrement [Fig.B], on peu aussi considérer que sous l'action de son propre poids, il s'enfonce (là on a quitté le modèle du volume parfait à masse nul... on est bien d'accord). On peut au passage dire :

Masse total - Masse du Volume = Masse utile.

Si on dépasse la masse utile, le parallélépipède coule (principe d'Archimède). C'est sur ce principe qu'est articulé le fonctionnement des docks flottants comme le montre le schéma plus haut !

A suivre : Volume et charge utile...